Design and Study of Machine Tools for the Fly-Cutting of Ceramic-Copper Substrates
Abstract
:1. Introduction
2. Design Principle of the Diamond Precision Fly-Cutting Device
2.1. Ceramic-Copper Substrate Composition
2.2. Fly-Cutting Processing Method
2.3. Fly-Cutting Principle and Accuracy Analysis
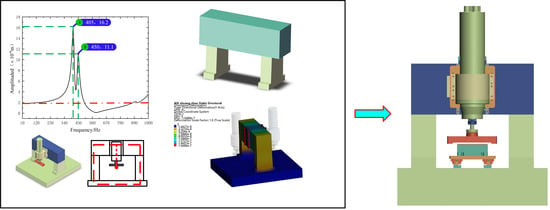
3. Design of the Ceramic-Copper Substrate Fly-Cutting Device
3.1. Form of the Installation’s General Layout
3.2. Design Indicators for Machine Tools
3.3. Structural Design of the Beam-Column Arrangement
3.4. Structural Design of the Flying-Cutting Disc Components
4. Measurement and Verification Experiments
4.1. Complete Machine Assembly
4.2. Measurement of Guideway Straightness
4.3. Fly Cutting Processing Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guzowski, B.; Rosowski, A.; Lisik, Z.; Jakubowska, M.; Sharp, M. The integration of optical interconnections on ceramic substrates. Microelectron. Eng. 2016, 157, 19–23. [Google Scholar] [CrossRef]
- Goto, T.; Matsubayashi, Y.; Akedo, J. Ceramic coating on rubber by aerosol deposition with cryogenic substrate cooling. Ceram. Int. 2024, 50, 892–896. [Google Scholar] [CrossRef]
- Zhu, J.; An, R.; Wang, C.; Wen, G. Fabrication of Al2O3-Mullite-AlN Multiphase Ceramic Layer on W-Cu Substrates for Power Semiconductor Packaging. IEEE Trans. Components Packag. Manuf. Technol. 2015, 5, 182–187. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, C.W.; Choi, J.J.; Ryu, J.; Kim, J.W.; Yoon, W.H.; Park, D.S.; Yoon, S.Y.; Ma, B.; Hahn, B.D. Next Generation Ceramic Substrate Fabricated at Room Temperature. Sci. Rep. 2017, 7, 6637. [Google Scholar] [CrossRef] [PubMed]
- Schubert, M.; Hahn, M.; Exner, J.; Kita, J.; Moos, R. Effect of substrate hardness and surface roughness on the film formation of aerosol-deposited ceramic films. Funct. Mater. Lett. 2017, 10, 1750045. [Google Scholar] [CrossRef]
- Ganesan, G.; Malayath, G.; Mote, R.G. A review of cutting tools for ultra-precision machining. Mach. Sci. Technol. 2022, 26, 923–976. [Google Scholar] [CrossRef]
- Lukin, E.S.; Anufrieva, E.V.; Popova, N.A.; Morozov, B.A.; Preobrazhenskii, V.S.; Bezlepkin, V.A.; Ukhvatova, L.S.; Brzhezinskii, G.V. Analysis of Surface Microstructure and Quality and Properties of Aluminum Oxide Substrates. Glass Ceram. 2011, 67, 271–276. [Google Scholar] [CrossRef]
- Andre, J.; Botrel, R.; Schunck, J.; Pinay, A.; Chicanne, C.; Theobald, M. Specific Adaptations of Mechanical Machining Processes for Laser Target Manufacturing. Fusion Sci. Technol. 2016, 70, 237–243. [Google Scholar] [CrossRef]
- Lyu, D.; Liu, Q.; Liu, H.; Zhao, W.H. Dynamic error of CNC machine tools: A state-of-the-art review. Int. J. Adv. Manuf. Technol. 2020, 106, 1869–1891. [Google Scholar] [CrossRef]
- Bougharriou, A.; Bouzid, W.; Sai, K. Analytical modeling of surface profile in turning and burnishing. Int. J. Adv. Manuf. Technol. 2014, 75, 547–558. [Google Scholar] [CrossRef]
- Liu, P.F.; Chen, W.Q.; Su, H.; Chen, G.D. Dynamic design and thermal analysis of an ultra-precision flycutting machine tool. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2018, 232, 404–411. [Google Scholar] [CrossRef]
- Yuan, J.C.; Li, J.S.; Wei, W.; Liu, P.K. Operational modal identification of ultra-precision fly-cutting machine tools based on least-squares complex frequency-domain method. Int. J. Adv. Manuf. Technol. 2022, 119, 4385–4394. [Google Scholar] [CrossRef]
- Lu, H.J.; Ding, Y.Y.; Chang, Y.; Chen, G.L.; Rui, X.T. Dynamics Modelling and Simulating of Ultra-precision Fly-Cutting Machine Tool. Int. J. Precis. Eng. Manuf. 2020, 21, 189–202. [Google Scholar] [CrossRef]
- Li, W.; Li, B.Z.; Yang, J.G. Design and dynamic optimization of an ultra-precision micro grinding machine tool for flexible joint blade machining. Int. J. Adv. Manuf. Technol. 2017, 93, 3135–3147. [Google Scholar] [CrossRef]
- Wang, H.; Li, T.J.; Sun, X.Z.; Mynors, D.; Wu, T. Optimal Design Method for Static Precision of Heavy-Duty Vertical Machining Center Based on Gravity Deformation Error Modelling. Processes 2022, 10, 1930. [Google Scholar] [CrossRef]
- Wang, T.Z.; Cheng, J.; Liu, H.N.; Chen, M.J.; Wu, C.Y.; Su, D.N. Ultra-precision grinding machine design and application in grinding the thin-walled complex component with small ball-end diamond wheel. Int. J. Adv. Manuf. Technol. 2019, 101, 2097–2110. [Google Scholar] [CrossRef]
- Yang, X.; An, C.H.; Wang, Z.Z.; Wang, Q.J.; Peng, Y.F.; Wang, J. Research on surface topography in ultra-precision flycutting based on the dynamic performance of machine tool spindle. Int. J. Adv. Manuf. Technol. 2016, 87, 1957–1965. [Google Scholar] [CrossRef]
- Lei, P.L.; Wang, Z.Z.; Shi, C.C.; Peng, Y.F.; Lu, F.; Liu, Z.H. Experimental study on the reliability and the precision maintenance of the ultra-precision grinding machine based on the key subsystem platforms. Int. J. Adv. Manuf. Technol. 2023, 124, 3923–3934. [Google Scholar] [CrossRef]
- Ding, Y.Y.; Rui, X.T.; Chang, Y.; Lu, H.J.; Chen, Y.H.; Ding, J.G.; Shehzad, A.; Chen, G.L.; Gu, J.J. Optimal design of the dynamic performance of the ultra-precision fly cutting machine tool. Int. J. Adv. Manuf. Technol. 2023, 124, 567–585. [Google Scholar] [CrossRef]
- Ding, Y.Y.; Rui, X.T.; Lu, H.J.; Chang, Y.; Chen, Y.H. Research on the dynamic characteristics of the ultra-precision fly cutting machine tool and its influence on the mid-frequency waviness of the surface. Int. J. Adv. Manuf. Technol. 2020, 106, 441–454. [Google Scholar] [CrossRef]
- Chen, G.D.; Sun, Y.Z.; Zhang, F.H.; An, C.H.; Chen, W.Q.; Su, H. Influence of ultra-precision flycutting spindle error on surface frequency domain error formation. Int. J. Adv. Manuf. Technol. 2017, 88, 3233–3241. [Google Scholar] [CrossRef]
- Asilturk, I.; Cunkas, M. Modeling and prediction of surface roughness in turning operations using artificial neural network and multiple regression method. Expert Syst. Appl. 2011, 38, 5826–5832. [Google Scholar] [CrossRef]
- Wang, J.H.; Yazawa, T.; Han, J.G.; Otsubo, T.; Kato, T. Study on improving machined surface accuracy using diamond fly cutting on an ordinary milling machine. Int. J. Adv. Manuf. Technol. 2022, 121, 8409–8421. [Google Scholar] [CrossRef]
- Azami, S.; Kudo, H.; Mizumoto, Y.; Tanabe, T.; Yan, J.; Kakinuma, Y. Experimental study of crystal anisotropy based on ultra-precision cylindrical turning of single-crystal calcium fluoride. Precis.-Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2015, 40, 172–181. [Google Scholar] [CrossRef]
- Sung, A.N.; Ratnam, M.M.; Loh, W.P. Effect of wedge angle on surface roughness in finish turning: Analytical and experimental study. Int. J. Adv. Manuf. Technol. 2014, 74, 139–150. [Google Scholar] [CrossRef]
- Kull Neto, H.; Diniz, A.E.; Pederiva, R. The influence of cutting forces on surface roughness in the milling of curved hardened steel surfaces. Int. J. Adv. Manuf. Technol. 2016, 84, 1209–1218. [Google Scholar] [CrossRef]
- Li, J.S.; Wei, W.; Huang, X.J.; Liu, P.K. Study on dynamic characteristics of ultraprecision machining and its effect on medium-frequency waviness error. Int. J. Adv. Manuf. Technol. 2020, 108, 2895–2906. [Google Scholar] [CrossRef]
- Bai, L.; Yang, Q.Z.; Cheng, X.; Ding, Y.; Xu, J.F. A hybrid physics-data-driven surface roughness prediction model for ultra-precision machining. Sci. China-Technol. Sci. 2023, 66, 1289–1303. [Google Scholar] [CrossRef]
- Tan, R.K.; Zhao, X.S.; Lin, F.T.; Jin, S.J.; Guo, X.M.; Chen, X.; Sun, T. Analytical modelling and experimental study of surface roughness in ultrasonic elliptical vibration assisted ultra-precision cutting of Ti-6Al-4 V alloy. Int. J. Adv. Manuf. Technol. 2023, 126, 1863–1875. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, X.S.; Li, G.; Zong, W.J.; Sun, T. Study regarding the influence of process conditions on the surface topography during ultra-precision turning. J. Manuf. Process. 2023, 102, 23–36. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Fan, J. Effect of KDP-Crystal Material Properties on Surface Morphology in Ultra-Precision Fly Cutting. Micromachines 2020, 11, 802. [Google Scholar] [CrossRef] [PubMed]
- Peterka, J. A New Approach to Calculating the Arithmetical Mean Deviation of a Profile during Copy Milling. Stroj. Vestn. 2004, 50, 594–597. [Google Scholar]




















| Typology | Fly-Cutting |
|---|---|
| Distance ravelled | Y-axis: 800 mm Z-axis: 5 mm |
| Guideway straightness error | Y-axis: 4 m mm Z-axis: 3 m mm |
| Minimum feed speed | Y-axis: 10 m/s Z-axis: 1 m/s |
| Spindle runout error | Spindle: m |
| Workpiece material | Copper |
| Spindle speed | 0–1000 rpm |
| Size of workpiec | |
| Workpiece roughness | Sa |
| Parametric | a | b | c | d | e | f | g | Frequency |
|---|---|---|---|---|---|---|---|---|
| Initial size (mm) | 0 | 75 | 300 | 450 | 440 | 220 | 220 | 405 Hz |
| Optimised size (mm) | 20 | 80 | 300 | 500 | 420 | 200 | 220 | 420 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, J.; Zhou, J.; Chen, X. Design and Study of Machine Tools for the Fly-Cutting of Ceramic-Copper Substrates. Materials 2024, 17, 1111. https://0-doi-org.brum.beds.ac.uk/10.3390/ma17051111
Zhang C, Sun J, Zhou J, Chen X. Design and Study of Machine Tools for the Fly-Cutting of Ceramic-Copper Substrates. Materials. 2024; 17(5):1111. https://0-doi-org.brum.beds.ac.uk/10.3390/ma17051111
Chicago/Turabian StyleZhang, Chupeng, Jiazheng Sun, Jia Zhou, and Xiao Chen. 2024. "Design and Study of Machine Tools for the Fly-Cutting of Ceramic-Copper Substrates" Materials 17, no. 5: 1111. https://0-doi-org.brum.beds.ac.uk/10.3390/ma17051111