Next Article in Journal
Liquid Crystal Elastomers for Biological Applications
Next Article in Special Issue
Promoting the Selectivity of Pt/m-ZrO2 Ethanol Steam Reforming Catalysts with K and Rb Dopants
Previous Article in Journal
Mesoporous Iron(III)-Doped Hydroxyapatite Nanopowders Obtained via Iron Oxalate
Previous Article in Special Issue
Improved Water–Gas Shift Performance of Au/NiAl LDHs Nanostructured Catalysts via CeO2 Addition
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 11
Issue 3
10.3390/nano11030812
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation of Local Mechanical and Chemical Properties via AFM as a Tool for Understanding the Formation Mechanism of Pulsed UV Laser-Nanoinduced Patterns on Azo-Naphthalene-Based Polyimide Films

by
Iuliana Stoica
1,*,
Elena-Luiza Epure
2,
Catalin-Paul Constantin
1,
Mariana-Dana Damaceanu
1,
Elena-Laura Ursu
1,
Ilarion Mihaila
3 and
Ion Sava
1,*
1
“Petru Poni” Institute of Macromolecular Chemistry, 700487 Iasi, Romania
2
Faculty of Chemical Engineering and Environmental Protection, “Gheorghe Asachi” Technical University, 700050 Iasi, Romania
3
Integrated Center of Environmental Science Studies in the North-Eastern Development Region (CERNESIM), “Alexandru Ioan Cuza” University of Iasi, 700506 Iasi, Romania
*
Authors to whom correspondence should be addressed.
Nanomaterials 2021, 11(3), 812; https://0-doi-org.brum.beds.ac.uk/10.3390/nano11030812
Submission received: 30 January 2021 / Revised: 15 March 2021 / Accepted: 19 March 2021 / Published: 22 March 2021
(This article belongs to the Special Issue Tuning the Physicochemical Properties of Nanostructured Materials through Advanced Preparation Methods)
Browse Figures
Versions Notes

Abstract

:
Aromatic polyimides containing side azo-naphthalene groups have been investigated regarding their capacity of generating surface relief gratings (SRGs) under pulsed UV laser irradiation through phase masks, using different fluencies and pulse numbers. The process of the material photo-fluidization and the supramolecular re-organization of the surface were investigated using atomic force microscopy (AFM). At first, an AFM nanoscale topographical analysis of the induced SRGs was performed in terms of morphology and tridimensional amplitude, spatial, hybrid, and functional parameters. Afterward, a nanomechanical characterization of SRGs using an advanced method, namely, AFM PinPoint mode, was performed, where the quantitative nanomechanical properties (i.e., modulus, adhesion, deformation) of the nanostructured azo-polyimide surfaces were acquired with a highly correlated topographic registration. This method proved to be very effective in understanding the formation mechanism of the surface modulations during pulsed UV laser irradiation. Additionally to AFM investigations, confocal Raman measurements and molecular simulations were performed to provide information about structured azo-polyimide chemical composition and macromolecular conformation induced by laser irradiation.

Graphical Abstract

1. Introduction

Polyimides (PIs) represent an important class of high-performance polymers that are exploited in a variety of applications due to their excellent physicochemical properties such as optical and thermal stability in combination with high glass transition temperature, low susceptibility to laser damage, and low dielectric constant value [1,2]. Moreover, polyimides have been investigated as potential materials in the fields of optoelectronics and photonics [3]. Particularly interesting are polyimides containing azobenzene units, which have already been investigated for photoinduced alignment in liquid crystal display [4], as photomechanical response materials [5], and for holographic diffraction grating recording [6,7,8,9,10,11]. The azo derivatives can be introduced into polymers in different ways: by polymerization reaction between monomers, which contain preformed azobenzene group (diamines or dianhydrides); by dissolving a guest chromophore in a polymer matrix; by attaching the chromophores covalently to the polymer chains; or by using of different nonconvalent intermolecular interactions (ionic interactions, coordination bonds, hydrogen bonds, π–π interactions) between the dye and the polymer backbone. The first method is the most used due to the better control of sequence chromophore distribution. The azobenzene-functionalized monomers can be the diamines or dianhydrides or both of them [3,12,13,14,15,16]. Many azodiamines have been obtained and used for the synthesis and characterization of the azopolyimides, usually containing substituted or unsubstituted azobenzene side chains. Thus, a broad range of azopolyimides, azo polyamide-imides, or azo polyester-imides have been published thus far [12,15,17,18,19]. The majority of polymers functionalized with azobenzene derivatives under the action of linearly polarized light undergo multiple reversible trans to cis photo-isomerization processes. A supramolecular organization process is generated as a result of the perpendicular alignment of the azobenzene molecules to the electric field vector, controlling the photo-induced optical anisotropy. Thus, the azo-polymer photo-fluidization due to the above-described phenomenon can appear in the exposed regions [20,21]. Moreover, the cyclic photo-isomerization can lead to a large-scale mass transport of the polymer chains, which appear as a surface relief grating (SRG) [13,14,22,23]. Mainly, this mass displacement can take place from UV laser-exposed areas to the unexposed areas. Recently, it was demonstrated that also an inverse mass displacement can occur, from the dark regions to the illuminated ones [24]. The arguments for the development of the azobenzene photoisomerization process by inversion or rotation are the subject of numerous molecular simulation studies [25,26,27,28]. A large number of articles track the computational characterization of these photocontrolled materials due to their prospective applications in different fields such as liquid crystals [29,30,31], optical data storage [32], photosensitive micelles [33], triggers in protein folding [34], and so on. Due to the complexity of the molecular migration phenomenon that induces the SRG formation process, the number of molecular studies is significantly lower [35,36,37].
Over time, in order to obtain well-defined and stable SRGs on azo-polymers, researchers have applied two main techniques, namely, pulsed and continuous UV laser irradiation. In the case of continuous laser irradiation, the apexes of the sinusoidal surface relief appeared in the unexposed regions. When pulsed UV laser irradiation was employed, the positions of the apexes were dependent on the laser fluence, being in the exposed regions when the fluence value was below a threshold, and in the unexposed regions when the fluence value was above this threshold, as mentioned in the literature data [24]. In a pulsed laser regime, the relief geometric parameters depend on several factors. The design of the high-quality phase masks and their characteristics (the material used in fabrication, the fabrication method, the type of the lattice grating structures, the number of pitches, the period of the lattice, the period accuracy and uniformity, the efficiency (%) of the phase masks) are mainly responsible for the resulted pattern aspect. The nanostructures can also be strongly affected by the experimental parameters of the pulsed laser irradiation method, such as the incident laser wavelength, the incident laser fluence, the polarization of the laser, the angle of incidence, the number of laser pulses, and the duration of one laser pulse. Last but not least, the generation of the SRGs is dependent of the chemical structure of the azopolymer, in terms of the backbone flexibility and position of the azo-group in the polymer chain (inducing certain architecture), the pristine film surface morphology subjected to pulsed laser nanostructuring, and the film thickness.
Many researchers have been focused on the progress in atomic force microscopy (AFM) techniques to characterize the polymer films at the nano-scale by recording the local mechanical behavior, especially the force response to approach, even simultaneously with the recording of the morphology [38,39]. Over the years, the progress of several research groups in data acquisition and signal processing has allowed manufacturers to develop this technique, under different names, such as pulsed force mode (PFM), tested by WiTec company (Ulm, Germany) for scanning force microscopy (SFM) systems from CSEM, Digital Instruments, Molecular Imaging, Park, Seiko and TopoMetrix [40], PeakForce Quantitative Nanomechanical Mapping (PeakForce QNMTM, referred to as QNM for brevity, by Bruker), HybriD Mode Atomic Force Microscopy from NT-MDT (Zelenograd, Moscow, Russia) [41,42,43], Quantitative Imaging (QI, by JPK Instruments), or PinPoint mode from Park Systems Corp. (Suwon, Korea) [44]. Each has different features. Fast force spectroscopy mapping via PinPoint mode was designed to prevent positional errors by simultaneously acquiring accurate height and force–distance information in the whole scanning area, while the cantilever tip is lifted at every pixel at a perpendicular angle from the sample surface.
In this context, our study focused on the investigation of a newly synthesized aromatic polyimide containing azo-naphthalene side groups with the aim to evaluate the local morphological, mechanical, and chemical properties via atomic force microscopy, especially in PinPoint mode, and confocal Raman spectroscopy. It is meant to provide a deep understanding of the formation mechanism of SRGs induced by pulsed UV laser on these azo-polyimide films, through phase masks, using different fluencies and number of pulses. Moreover, this article attempts to correlate the macroscale behavior of this azo-naphthalene-based polyimide during photoisomerization with the one from the atomic level simulating certain polymeric systems with a different content of the cis isomer. The application of quantitative nanomechanical properties (i.e., modulus, adhesion, deformation) acquired with highly correlated topographic registration using PinPoint mode to describe the formation of nanostructured azo-naphthalene-based polyimide surfaces has not been reported yet in the literature to the best of our knowledge. The molecular simulation and confocal Raman spectroscopy complete this study, which promises to significantly advance the research in this field beyond the state of the art.

2. Materials and Methods

2.1. Material

An aromatic diamine containing the azo group (-N=N-) pendent to the triphenylmethane core was synthesized by the Williamson reaction of 4-[bis-(4-amino-3-methyl-phenyl)-methyl]-phenol with 3-[4-naphthalen-1-ylazo)-phenoxy]-bromopropane. Details regarding the preparation of this azodiamine and the corresponding intermediates have been recently reported elsewhere [45]. 4,4′(Hexafluoroisopropylidene)diphthalic anhydride (6FDA) was purchased from Aldrich and used as received. The azopolyimide has been synthesized by the polycondensation reaction of 6FDA with the above mentioned azodiamine by using a procedure previously reported [12,45]. The structure of the azo-naphthalene-based polyimide is shown in Figure 1. The thickness of the azo-naphthalene-based polyimide films, measured using a profilometer, was 3094–3117 nm, the average value being 3.10 ± 0.01 μm.
As previously reported in [45], the irradiation with UV light of 365 nm will induce the photoisomerization of the trans isomer to the cis isomer. The intensity of the absorption bands located at 384 nm (due to the π → π* transitions in the trans isomer) decreased progressively as the irradiation time advanced, being assisted by the increase of the absorption band corresponding to the π → π* and n → π* transitions in the cis isomer, located at approximately 290 and 472 nm, respectively. Moreover, the corresponding isosbestic points were found at 325−326 and 450−459 nm, and the absorption coefficient was 1.1143 × 104 cm−1. The absorption coefficient has been calculated by using the equation: k = 2.303 A/d, where A is the absorbance and d is the thickness of the sample. Futhermore, the detailed evaluation of cis–trans thermal isomerization was carried out by UV–VIS spectroscopy both in solution and in solid state for the starting azodiamine monomer and corresponding azopolyimide, as it was largely presented in reference [45]. The thermal relaxation induced the total recovery of trans isomer after 2700 s. The thermal relaxation was reflected in the gradual increase of the bands at 384 nm (π → π* transitions, trans isomer) and the progressive decrease of the bands at 290 nm (π → π*) transitions, cis isomer) and 472 nm (n → π* transitions, cis isomer) during exposure at 70 °C for different intervals of time.

2.2. Molecular Simulations

The molecular dynamics simulations were performed with Materials Studio 4.0 software [46]. First, the structural units corresponding to the trans and cis isomers were built. These structural units were minimized through ab initio calculations within the DMol3 module using the Perdew-Wang PWC functional until fulfilling a 2 × 10−5 Hartree energy convergence. Subsequently, 3 polymer chains of 10 structural units each were built, with different content of cis isomer: AzoPI (with 15% cis groups), AzoPI_50%cis (with 50% cis groups), and AzoPI_100%cis (with 100% cis groups). The cis azo units were randomly distributed along the polymer chain. Both the structural units and the polymers were minimized with the Forcite module using the Dreiding force field. Three-dimensional amorphous structures were generated using the Amorphous Cell module. Each cell was built to contain three polymer chains of the same kind, at a density of 1 g/cm3, at 298 K. The final structures were obtained according to the following protocol: (step 1) minimization (energy convergence 1 × 10−4 kcal/mol), (step 2) 2 anneal cycles that were driven in the range of 300–800 K for 40 ps, (step 3) compression/constriction the cell by molecular dynamics (NPT ensemble (constant number (N), volume (V), and temperature (T); T is regulated via a thermostat; pressure (P) is regulated), T = 298 K, Berendsen thermostat and barostat) until the density reaches a value around 1.2 g/cm3, (step 4) equilibration of the cell through an NVT dynamics (constant number (N), volume (V), and temperature (T); T is regulated via a thermostat, pressure (P) is unregulated) for 500 ps (T = 298K, Nose thermostat). Achieving constant values for the density-time curves in NPT stage and temperature/energy-time in NVT-MD stage indicates that the system is stable and has reached an equilibrium value. Data collection was performed after another 200 ps of dynamic simulations in NVE ensemble (constant number (N), volume (V), and energy (E); T is regulated via a thermostat, pressure (P) is unregulated), at T = 298 K.

2.3. Laser Patterning

In order to induce micro/nano structuration on the azo-polyimide surface, we used the setting presented in Figure 2. A pulsed Nd:YAG laser (Brilliant B from Quantel) working at third harmonic (355 nm wavelength), with a diameter of 5 mm. The laser was horizontally polarized (s-polarized), meaning that its light oscillated along a horizontal plane. The electric field vector was perpendicular to the plane of incidence, to the direction of gravity, and to the direction of light propagation. In this way, the grating region was uniformly illuminated. This choice can be motivated on the basis of observations of Miniewicz and collaborators [47], according to which the grating strength in the case of s-p inscription attains higher values. The pulse duration of 6 ns was chosen. The pulse repetition rate was 10Hz. The aperture of 5 mm laser beam was enlarged until 15 mm, by placing a beam expander with a fixed ratio of 3×. A diffraction phase mask (Edmund Scientific Co., Barrington, NJ, USA) with a thickness of 76 μm and 1000 grooves per mm was used. The linear diffraction grating period was about 1 μm. After passing through the diffractive optical element, the laser beam generates an interference field in its proximity, leading to a laser interference pattern on the azo-polyimide surface, placed after the phase mask, producing features with the pitch of the same order of magnitude. The quartz plate placed between the phase mask and the sample had a thickness of 1 mm. Two incident fluences, namely, 10 mJ/cm2 and 45 mJ/cm2 (measured after beam expander), and two different numbers of pulses, namely, 10 and 100, were used. Therefore, the samples were named using the label AzoPI i/j, where i is the incident fluence and j is the number of irradiation pulses, as follows: AzoPI 10/10, AzoPI 10/100, AzoPI 45/10, and AzoPI 45/100.

2.4. Measurements

The AFM investigations on the nanostructured azo-polyimide films were performed in semi-contact mode, in the atmospheric conditions, at room temperature, on a surface area of 10 × 10 µm2, using a Scanning Probe Microscope Solver Pro-M from NT-MDT, Russia, using a high-resolution “golden” silicon AFM probe NSG01 (NT-MDT, Zelenograd, Moscow, Russia) with a typical curvature radius of 10 nm and the free resonant frequency of 90.5 kHz. AFM data acquisition and analysis were performed using Nova software from NT-DMT. The tridimensional parameters were calculated using Image Analysis 3.5.0.19892 software. Nanomechanical measurements were made on a Park NX10 Atomic Force Microscope (Park Systems Corp., Suwon, Korea), using PinPoint Nanomechanical mode, which allowed us to obtain sample’s stiffness mapping through force–distance curves acquired at each pixel over the entire scanning area (of 1 × 5 µm2 in our case). Thus, the quantitative nanomechanical properties (i.e., modulus, adhesion, deformation) of the nanostructured azo-polyimide surfaces were acquired with highly correlated topographic registration. In order to provide the most accurate mechanical properties data, we carefully selected the Force Modulation Mode - Reflex Coating (FMR) probe (Park Systems Corp., Suwon, Korea) with a force constant of 2.8 N/m and resonance frequency of 75 kHz according to the relative stiffness of their cantilever when compared to that of the sample, so that it can offer immediate response to any changes on the surface’s material properties. The scanning frequency was 0.5 Hz, and the scanning speed was 5.0 µm/s. Besides AFM investigations, supplementary confocal Raman measurements (laser source: 632.8 nm, 50 mW; CCD detector) performed using inVia Renishaw Raman confocal microscope (Renishaw, UK) were used to provide information about structured azo-polyimide chemical composition and macromolecular conformation. Spectra were recorded in backscattering geometry using a 50× objective. Spectral manipulations such as baseline adjustment, smoothing, and normalization were performed with the WiRE 3.3 software (Renishaw, UK).

3. Results and Discussion

Imaging the distribution of local mechanical properties at the nanoscale can significantly advance research on exciting soft materials relevant for optoelectronic applications [48]. In our case, the SRGs were produced using phase masks through pulsed laser irradiation, with a maximum light fluency lower than the ablation threshold of the material. This method employs a diffractive optical element (phase mask) for precise spatial modulation of the UV laser writing beam. In order to obtain the interference pattern, only the zero (0) and plus and minus first diffraction orders (±1) were considered. When a UV laser beam was incident on the phase mask, the zero-order diffracted beam was minimized. Furthermore, the plus and minus first diffracted orders were enlarged as much as possible [49]. Because of the very short irradiation times (6 nanoseconds) used in the pulsed mode, the mechanism responsible for the periodic SRGs profile generation involves the fringe pattern produced by the interference of the diffracted beams. They act through two possible mechanisms, namely, a very fast supramolecular reorganization process, induced by the azo-groups dipole orientation [50], and material photo-fluidization, induced by the trans–cis isomerization process of the azo-segments in the exposed regions [20,24,51]. This competes with the larger proper volume required by the cis conformation [52]. None of the models concerning the azo-polymers surface nanostructuration mechanisms proposed until now completely explain the surface relief formation, although a consensus has been reached—the azonaftalene dipoles orientation probably induce a more organized and compacted structure, having as a result a material contraction in the light-exposed regions with the generation of grooves in the dark areas [22]. Thus, it is considered that the highest intensity of the interference pattern corresponds to the valley of SRGs, due to the mass displacement from exposed to unexposed regions, and inverse mass displacement, from uncovered to covered regions [20,24,53,54]. On the other hand, it should be mentioned that the assignment highest intensity of the interference pattern corresponds to the valley of SRGs is material-dependent and cannot be ascertained from the data presented in this paper, but was previously demonstrated by direct observations of Hurduc and collaborators 20] who proposed a mechanism for SRG formation during laser irradiation involving at least three processes: (1) the polymer photofluidization in illuminated regions, (2) the mass displacement from illuminated to dark regions, and (3) the inverse mass displacement from dark to illuminated regions, on the basis of the performed amplitude modulation-frequency modulation atomic force microscopy (AM-FM AFM) viscoelastic mapping before, during, and after light irradiation.

3.1. AFM Nanoscale Morphological Analysis

The occurrence of the SRGs induced by the UV laser irradiation on azo-polyimide surface was highlighted using AFM investigations. Figure 3 presents the height 3D AFM images and the corresponding cross-section profiles obtained for the azo-polyimide films irradiated with different laser energy density/number of pulses of irradiation, as follows: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h). According to the height AFM images, Figure 4 depicts the height histograms and surface bearing area ratio curves of the azo-polyimide films irradiated using different laser energy density/number of pulses of irradiation: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h).
The anchoring of the azo group through an aliphatic spacer on the polyimide chains with flexible conformations given by the presence of hexafluoroisopropylidene groups induced a high isomerization/structuring capacity, transposed in the generation of repetitive surface structures through the phase mask, even at low energies and a small number of pulses. As can be seen in Figure 3a,b, from the AFM 3D image and the corresponding cross-section profile, by using an energy density of 10 mJ/cm2 and 10 pulses of irradiation, we found that the SRGs were not so visible, being only a few nanometers high. At this low energy, as the number of pulses increased, the structures became wider and better highlighted, although their height did not differ much from those obtained by using the small number of pulses (Figure 3c,d). Analyzing the profile diagram of the structured sample with higher energy density of 45 mJ/cm2 and using 10 pulses of irradiation, we observed a very good uniformity of the SRGs’ appearance, with the amplitude of the modulation being ≈50 nm (Figure 3e,f). This was due to the great mobility of the azo group in the side chain and flexibility of the main chain, as well as the existing free volume. Consequently, the polymer responded better to a high energy density of 45 mJ/cm2 and a small number of pulses (10). Moreover, it can be observed that in this case the SRGs were narrow, as in the previous case, when a small number of irradiation pulses were used. As the energy was increased, the repetitive structures became more and more defined, increasing in height with the increase of the number of pulses until 100 nm (Figure 3g,h) as observed from the cross-section profiles. It seemed that from the structural uniformity point of view, the irradiation with high energy and small number of pulses was the most indicated. At large number of pulses (100), their aspect was a corrugated one, as can be seen from the cross-section profile (Figure 3g). The obtained image suggests the occurrence of possible phenomena that may be due to surface reorganization mechanisms (Figure 3h) or to additional nanostructuring of the formations. This complex high-amplitude morphology may be an indication that the structured sample acted itself as a diffractive element—it generated further diffraction orders that gave shorter periods (higher harmonics) to the holographic irradiation pattern. The response of the material after irradiation may have been due to the mechanisms of reorganization on the surface or induced by the appearance of the photo-fluidization state. Photo-fluidization can become significant, especially when using a large number of pulses. However, regardless of the mechanism of the surface organization, due to the conformational changes that occur in the azo-polyimide during irradiation, it is difficult to assess the accurate response to the phase mask laser irradiation process of this material. In addition, according to Viswanathan et al. [55], since mechanical forces may also act in the bulk of the film, it is possible that the orientation grating extends also throughout the thickness of the material.
The values obtained for the root mean square roughness (Table 1) were influenced by the SRGs aspect and amplitude, following the same trend. In this way, it was observed that Sq increased as the energy/number of pulses increased.
The aspect of the height histograms (Figure 4a,c,e,g) also describes the surface features created by the phase mask UV laser irradiation by means surface skewness (Ssk) and coefficient of kurtosis (Sku) (Table 1), indicating also the distribution of the relief on areas of interest: the valley zone, the core zone, and the peak zone. Details regarding their meaning can be found in Appendix A.
The hybrid parameter surface area ratio (Sdr), calculated as the ratio between the area of the real developed surface and the area of the projected surface, can be used to describe the complexity of the surface. This parameter has an important role in controlling the surface properties of the materials envisaged for use in electronics [56], being a key factor for measuring the performance. Analyzing the data from Table 1, one can conclude that the surface complexity increased with the increase of the laser energy density due to the appearance of well-defined SRGs. The most complex surface was obtained for AzoPI 45/100 sample, induced by the supplementary nanostructurations of the SRGs formations, visible in Figure 3g,h.
The values of the spatial parameter surface texture direction index (Stdi) (displayed in Table 1 and calculated examining the 3D AFM height images and the corresponding angular spectra) were indicators of whether or not a surface has a preferential orientation of its features, thus denoting the anisotropy/isotropy of the morphology. Stdi close to 1 indicates that the sample surface is isotropic, with a random surface texture that does not have any texture that stands out, with no preferential orientation and presenting identical characteristics regardless of the direction of measurement. Meanwhile, Stdi close to zero shows a dominant direction of the surface morphology [14,57]. This can indicate an oriented surface or a periodic structure. In this case, the surface is considered to be anisotropic. Therefore, for all nanostructured samples, the values of about 0.2–0.4 attributed of this spatial parameter denote the anisotropy of the morphology induced by the oriented SRGs under pulsed UV laser irradiation. Moreover, AzoPI 45/10 sample shows the highest degree of orientation and organization, indicated by the lowest value of Stdi, namely, 0.193. This information is very important in describing the anisotropy of the morphology, used in electronic applications, where the controlling of the alignment is necessary.
Upon computation by inversion of the cumulative height distribution histograms, division into zones (Figure 4a,c,e,g), the surface bearing area ratio curves or Abbott curves (Figure 4b,d,f,h) were used as the basis for calculating the functional indexes (Sbi, Sci, Svi) and functional volume parameter (Vmp, Vmc, Vvc, Vvv) [58].
These parameters, presented in Table 1, are of great importance for the pursued applications. Low surface bearing index values (Sbi < 0.608) [57] obtained for AzoPI 10/10, AzoPI 10/100, and AzoPI 45/100 films revealed surfaces with low bearing capacity. This fact is also supported by low values obtained for the peak material volume. Instead, AzoPI 45/10 sample has bearing index higher than 0.608, indicating a good bearing capacity. In the core zone, Sci is sensitive to both occasional high peaks and occasional deep valleys. AzoPI 10/10 and AzoPI 10/100 have a low core fluid retention index (Sci < 1.56) [57], induced also by the low values of the core material and void volumes, while AzoPI 45/10 and AzoPI 45/100, due to their complex morphology and high core material and void volumes, have a high core fluid retention index (Sci > 1.56) [57]. The analyzed surfaces with relatively few deep valleys have low valley fluid retention index (Svi < 0.11) [57] due to low valley void volumes.
In this way, the pattern can be designed by controlling the experimental parameters, and by calculating these parameters that describe the obtained morphology, we can select a certain pattern for a special desired electronics manufacturing application.
The topography does not provide the difference in mechanical properties (such as elasticity, adhesion). AFM phase imaging can provide mechanical properties distribution using qualitative contrast. On the other hand, force–distance spectroscopy records mechanical data quantitatively by indenting a cantilever tip on the sample surface one point at a time. In our case, the analysis of the mechanical characteristics of the newly formed nanogrooves required to acquire the distribution image and the quantitative data simultaneously.

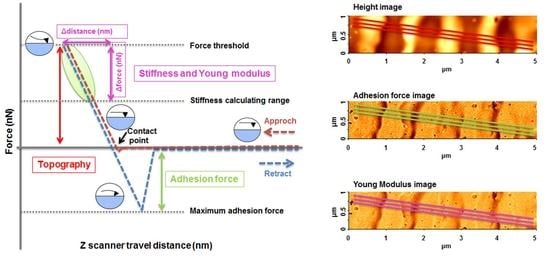
3.2. Nanomechanical Characterization Using AFM PinPoint Mode

PinPoint Nanomechanical mode was designed to prevent positional errors by simultaneously acquiring accurate height and force–distance information in each of the 256 × 256 pixels in the whole scanning area, thus preventing the occurrence of the artifacts and positional errors in force–distance spectroscopy and topographical data. In Figure 5 and Appendix B, we present the working mechanism of PinPoint Nanomechanical mode, describing the generation of the map of the sample’s stiffness/elasticity and deformation depth from the surface concomitantly obtained through the adhesion force map with the topographic sample information [59,60,61,62,63,64].
Figure 6, Figure 7 and Figure 8 show the PinPoint combined height, adhesion force, deformation, and Young’s modulus AFM images and corresponding cross-section profiles in the case of pristine (Figure 6) and irradiated azo-polyimide with a laser energy density of 45 mJ/cm2 and either 10 pulses (Figure 7) or 100 pulses (Figure 8). The last two samples were selected for this kind of measurement because the generated modulations were very well defined, facilitating the investigations in different positions of interest (on the top hills, middle slopes, base, and bottom valleys of the SRG, as indicated in Figure 5). Each profile was an average of the profiles in the band highlighted in the images, excepting the case of the pristine sample, where the surface was random.
As seen in Table 2, the pristine AzoPI presented an average adhesion force of 12.6 ± 0.8 nN, deformation of 5.1 ± 0.2 nm, and Young’s modulus of 294.8 ± 20.5 MPa. After the SRG formation as a result of pulsed UV laser irradiation, these nanomechanical characteristics were found to be different, depending on the region of the modulation where the measurements were made, namely, on SRG top hills, middle slope, bottom valleys, and baseline, as indicated in Figure 5. Thus, various values of nanomechanical parameters were obtained in these different regions, mostly induced by the density of the material, but not limited to it.
As mentioned above, the valley of the SRGs corresponds to the highest intensity of the UV laser irradiation through the phase mask. In this region, the macromolecules containing azo groups in the lateral chains undergo photo-isomerization during irradiation, when transitions from stable trans state to metastable cis state occurs along with changes in the molecular length and the dipole moment (Figure 9) [65]. This phenomenon will engender a localized substantial nanoscale stress, requiring more free volume for the local motion of azo groups from the lateral chain in cis configuration [52] and movement of the whole azo-polyimide backbone, inducing a dilatation effect and a continuous disturbance of the localized stress field [66].
Figure 9 shows three different stages of the system: stage I with polymer chains having azo-naphthalene modified in cis conformation in proportion of 15%, stage II with 50% azo- naphthalene groups in cis conformation, and stage III having all azo-naphthalene segments in cis form.
Molecular simulations have confirmed this expansion effect by higher values of the volume occupied by the polymer chains, Vo, for the AzoPI in stage II compared to the stage I and the stage III (Table 3). Regardless of the mechanism involved in the photo-isomerization, rotation around the azo group, or inversion through one of the nitrogen nuclei, we found that a sufficiently large free volume was required to allow this mechanism, avoiding steric hindrances. It was found that the same system, AzoPI, had the largest free volume fraction in stage II. The free spaces between atoms provided the empty space useful for the movement of the molecular chains, and thus ensured the evolution towards the state III of the system.
In order to characterize the average configuration of a chain, we calculated the structural end to end distance (ree) parameter. It was found that this parameter increased from stage I to stage II (Table 3) when the maximum value was reached, after which a decrease took place (stage III). In this case, first, the macromolecular chain stretched and then adopted a coil structure more compact than the starting one.
Cohesive energy density (CED) is a measure of the binding energy of the polymers relative to the unit volume. The CED also indicates the mixing degree of the polymer chains. Comparing the results from Table 3, we observed that the structure of AzoPI in stage II had the lowest cohesive energy density.
Saphiannikova et al. [67] demonstrated that the sign of the force induced by light is very sensitive to the molecular architecture, and therefore an effect of local extension occurs for amorphous azo-polymers. Consequently, due to the stress release in the UV laser-exposed region, a sudden modulating of the morphology takes place.
A very interesting phenomenon was observed. On SRG middle slopes, the average adhesion force and Young’s modulus were strongly reduced, simultaneous with the increases of the deformation (Table 2). Here, it seemed that the azo-material was softer, which may be related to a photo-induced reduction of the density [67,68,69]. Moreover, the molecular modeling data revealed that the structure with 50% of azo groups in cis conformation had the lowest value of cohesive energy density. With the decrease of the cohesive interactions, the force necessary to produce a deformation will decrease, meaning the decrease of Young’s modulus.
Moreover, it was observed that, although in the case of Azo-PI 45/100, when the number of pulses of irradiation was higher than those used in the Azo-PI 45/10 case, still the adhesion force and Young’s modulus were smaller. This is probably due to the higher number of trans–cis–trans photo-isomerization cycles of the azo-moieties that induce a material flow and implicitly a very weak plasticization. It is well understood that the material flow (as a dynamical process where material is moving) could not be directly measured here. However, plasticization could be inferred, with this being related to a change in the elastic properties (softening or hardening).
At the baseline, and especially on the bottom of new formed SRG, there was a high concentration of azo-naphthalene moieties in the cis state, which in both studied cases AzoPI 45/10 and AzoPI 45/100 changed the mechanical properties (see Table 2), slightly increasing the Young’s modulus, comparative to that obtained for the pristine sample. Hardening of the azo-polymer, as a result of an initial plasticization, was induced by the presence of a high population of cis fraction. The high density of cis isomers leads to an increase in the strength of intramolecular interactions in this region and also stronger interactions with the surrounding environment than trans isomers [70], a fact also proved by the CED values determined by the molecular dynamic simulations (Table 3). Thus, the local values of the Young’s modulus of the azo-polyimide are expected to vary with the concentration of cis isomers.
The rigidity, the hardening of the polymer, correlates at the microscale level with the mobility of the chains. The mean square displacement (MSD) function characterizes the movement of polymer chains by measuring the deviation of the position of a particle at a time (t) from the position it had at the reference time (0):
MSD   ( t ) = [ r ( t ) − r ( 0 ) ] 2
According to Figure 10, the mobility of the backbone of AzoPI in stage III was the lowest, indicating that this system with all azo groups in the cis configuration was the most rigid. The intensity of the backbone movements for AzoPI in stage I and stage II were found to be similar over time. As expected, the azo segments (C–N=N–C) belonging to the polymer side chains had wider movements compared to the mobility of the main rigid chains. It was observed that the azo segments in the AzoPI in stage III chains mimicked the behavior of the chains from stage I, having much lower mobility compared to the other azo segments. The mobility of the azo segments belonging to the AzoPI polymers in stage I and II was approximately the same, reaching at 200 ps the segments connected to AzoPI in stage I to have a slightly higher motion than those connected to AzoPI in stage II.
Moreover, the azo-naphthalene dipoles orientation can determine a more organized and condensed structure, having as a consequence the material contraction in the exposed regions, leading also to an increase of the hardness. If we consider the side azo segments (C–N=N–C) belonging to the three polymeric systems, the distribution of the dipole moment along the Cartesian axes as a function of time is represented graphically in Figure 11. However, we must specify that in the simulations the azo groups were left free to evolve, without any constraint of the dihedral angles.
The photoinduced molecular reorientations are those that dictate the direction and modulus of the dipole moment. The different values of the dipole moment obtained in our three considered cases indicate changes in the geometry and polarity of the azo segment over time. As can be seen, the dipole of the group defined by the azo segments was different from one stage to another, being dependent on the rigidity and geometry of the chain. On the other hand, the cumulative effect of lateral group movement can cause changes in the conformation of the molecule. By averaging the values of the dipole modulus along the 200 ps, we obtained the following values for the azo segments: μAzoPI = 3.7 D, μAzoPI_50%cis = 5.4 D, and μAzoPI_100%cis = 8.6, following the natural evolution of the modulus growth with the transition from the trans to the cis isomer.
As mentioned earlier, as a consequence of the interaction with the pulsed UV laser, during the trans–cis isomerization, the azo groups induce a very high pressure that determines the azo-polyimide to be able to develop high expansion forces during mass transport [52,71], which is liable for the irreversible deformations leading to SRG formation. In this stage, we found a certain state of matter, with a special feature, namely, extremely high viscosity and very low speed of polyimide chain displacement, on the strength of trans–cis–trans motion of azo-segments, that act as molecular motors [21]. The measurements performed on the peak of the sinusoidal pattern induced by this mass transport towards the lateral, together with the elastic material deformation determined by the supramolecular reorganization process, apparently indicated that no reaction takes place in this region (as a result of being protected by the mask). Thus, since these areas are rich in lateral chain azo groups in trans configuration, the values of the elastic modulus were close to that obtained for the pristine azo-polyimide (Table 2).
Essentially, during the dynamics of SRG formation process, there is a phenomenon in the variation of the material density [72].

3.3. Evaluation of the Local Chemical Properties

Raman spectroscopy was used to identify the signature of the aromatic azo group grafted on the polyimide chains before and after irradiation. According to literature data, the azo (-N=N-) stretching band (-N=N-) has strong intensity with the trans form absorbing in the range of 1465–1380 cm−1 and cis form around 1510 cm−1 [73,74].
As can be seen in Figure A1, all the SRGs resulted after the treatment of azo-polyimide films with UV-pulsed laser radiation in different conditions showed the same strong absorption bands at 1449 cm−1 due to the distinct vibrational band (νN=N) of the polymer chromophore that corresponded to the trans isomer. A very small absorption band around 1510 cm−1 could be observed as well for all irradiated samples, being associated with the vibrational band of the azo-group in cis form. It was obvious that this small absorption band slightly evolved with the increase of the incident fluence energy and number of pulses used for laser irradiation. Meanwhile, the vibrational band attributed to C–N bond (νC-N) was identified for all azo-polyimide films at 1138 cm−1. Besides the appearance of the small absorption band around 1510 cm−1 associated with the vibrational band of the cis isomer formed after irradiation, the Raman spectra of irradiated films were not significantly altered as compared to that of the pristine sample, indicating that no chemical modification or degradation of the polyimide occurred during the irradiation. Accordingly, the changes detected in AFM measurements at the nanoscale were induced by conformational transitions, as also predicted by molecular modeling.

4. Conclusions

The aim of this study was to provide new insights regarding the formation mechanism of pulsed UV laser-nanoinduced patterns on azo-naphthalene-based polyimide films by evaluating the morphological, statistical, local mechanical, and chemical properties via AFM, in correlation with the molecular modeling. The quantitative nanomechanical properties (Young’s modulus, adhesion, deformation) of SRGs using the AFM PinPoint method were acquired with highly correlated topographic registration. The experimental evaluations highlighted different values of nanomechanical parameters obtained in different regions of the patterned relief. These were induced by re-organization of the matter by azo-naphthalene dipoles orientation and material photo-fluidization induced by repeated trans–cis isomerization of the azo-segments.
Attempts have been made to explain experimental phenomena by molecular modeling. The photoisomerization phenomenon was studied using three systems in which the content of cis isomers was gradually increased. Although the variations of the statistical and dynamic parameters such as the fractional free volume, end to end distance, mean square displacement, or dipole moment were small from one system to another, their evolution followed the same behavior as that observed at the macroscale during the photo-isomerization process. It was found that polymers with 50% azo groups in cis had either a maximum or a minimum peak of the calculated parameters. The low mobility of the chains with a maximum content in the cis isomer could explain the phenomenon of azopolymer hardening due to the photoisomerization process.
In addition, confocal Raman measurements evidenced no significant spectral changes, except for the slight increase of the absorption band due to the cis isomer evolution, demonstrating their origin in the polymer conformations before and after irradiation rather than in the polyimide chemical modifications.

Author Contributions

Conceptualization, I.S. (Iuliana Stoica); methodology, I.S. (Iuliana Stoica) and E.-L.E.; validation, C.-P.C., M.-D.D., and I.S. (Ion Sava); formal analysis I.S. (Iuliana Stoica) and E.-L.E.; investigation, I.S. (Iuliana Stoica), E.-L.E., E.-L.U., and I.M.; resources, I.S. (Iuliana Stoica), E.-L.E., C.-P.C., M.-D.D., E.-L.U., I.M., and I.S. (Ion Sava); data curation, I.S. (Iuliana Stoica), E.-L.E., and E.-L.U.; writing—original draft preparation, I.S. (Iuliana Stoica), E.-L.E., and I.S. (Ion Sava); writing—review and editing, I.S. (Iuliana Stoica), E.-L.E., C.-P.C., M.-D.D., E.-L.U., I.M., and I.S. (Ion Sava); visualization, I.S. (Iuliana Stoica); supervision, I.S. (Iuliana Stoica) and I.S. (Ion Sava); project administration, I.S. (Iuliana Stoica); funding acquisition, I.S. (Iuliana Stoica). All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Fellowship Program L’Oreal–Unesco “For Women in Science”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data is available on the request from corresponding author.

Acknowledgments

This work was funded by the National Fellowship Program L’Oreal–Unesco “For Women in Science”. We also thank Victor Bergmann, Application Director at Park Systems Europe (Mannheim, Germany), for his guidance in PinPoint AFM technique.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

The use of two 3D topographic parameters, namely, surface skewness (Ssk) and coefficient of kurtosis (Sku), allowed us to measure the departure from a Gaussian distribution of surface heights, emphasizing on one hand the degree of symmetry of the surface heights reported to the mean plane (Ssk), and on another hand the spread of the newly created structures in relation with the whole surface morphology (Sku). Consequently, the value of the skewness was influenced by the surface dislevelment, which can be above (negative skewed) or below (positive skewed) the mean surface height, implicitly being sensitive to occasional deep valleys or high peaks. The negative skewness obtained for AzoPI 10/100 sample (Table 1, Figure 4c) indicated surfaces with truncated peaks or occasional deep valleys (as seen in the cross-section profiles from Figure 3d). The positive skewness, calculated for AzoPI 10/10, AzoPI 45/10, and AzoPI 45/100 (Table 1, Figure 4a,e,g), revealed profiles with valleys filled in, or occasional high peaks, as pictured in Figure 3b,f,h by the cross-section profiles. The lower positive value of the kurtosis (Sku < 3) obtained for the homogeneous periodic AzoPI 45/10 sample (Table 1) indicated that the surface was platykurtic (Figure 4e), presenting a bumpy morphology with a relatively even distribution of heights above and below the mean height (as seen in Figure 3f of the cross-section profile). Thus, the valley zones and the up hills were well-defined. The higher positive values of the kurtosis (Sku > 3) obtained for AzoPI 10/10, AzoPI 10/100, and AzoPI 45/100 (Table 1) suggest leptokurtic surfaces (Figure 4a,c,g), with surface relief gratings with spiky morphologies (as observed also from the cross-section profiles from Figure 3b,d,h).

Appendix B

Along with 3D imaging at the nanoscale, nanomechanical properties (including adhesion, hardness, etc.) measurement on the sample surface at nN-scale via force–distance (F-d) spectroscopy by using a cantilever tip to probe the sample is one of the most well-known functions of AFM. This technique, widely used in domains such as physics, chemistry, and materials science dealing with nanoscale research, generally implies firstly acquiring a reference map of the topography data of a sample, on which the force–distance measurements are subsequently be made in the regions of interest after a preliminary alignment. Still, it is hard to prevent both positional errors in force–distance spectroscopy data and topographical data, as well as the artifacts induced by the adhesive tip–soft sample interaction. This is why PinPoint Nanomechanical mode was designed to prevent these positional errors by simultaneously acquiring accurate height and force–distance information in each of 256 × 256 pixels in the whole scanning area, while moreover preventing the cantilever tip from grabbing additional material from the surface when it travels to the next pixel position by lifting it at every pixel at a perpendicular angle from the sample surface. For this, some preset parameters are necessary. One of the most important is the control height, which is determined in the AFM cantilever retraction process from the sample surface in its movement between pixels and is dependent on the features of the sample surface. For example, if the surface heights are small, the control height must be small, and vice versa. However, in some cases, if the surface sample has small heights, but is tacky, then the height control must be suitably enlarged in order to separate the tip from the sample in anticipation of the switch to the next pixel. Other necessary preset parameters are the stiffness threshold (which establishes the force frequently acting on the surface sample), the approach and retract time, the XY pixel-to-pixel movement time, the pre-approach delay for determining a scanning speed, and the lift height. Thus, an optimized surface morphology providing precisely the height information is determined.
In the first instance, PinPoint mode imaging can generate an adhesion map using the maximum adhesion force value by acquiring in each pixel the adhesion force (Fadh) between the structured formations and silicon cantilever, calculated from each force–distance curve (as the one from Figure 5) as a linear function of the probe displacement relative to the sample surface along to the Z-axis, according to Hooke’s law, expressed by
F adh = − k Δ x ,
where k is cantilever stiffness and Δx is deflection of the cantilever in rapport with azo-polyimide SRG.
The sample’s stiffness/elasticity (Young’s modulus) can be acquired, similar to the force–distance spectroscopy procedure, from the slope of the force–distance curve taken at each pixel, from the point of contact to the deflection threshold, as seen in Figure 5, fitted with the Hertz model [59,60,61]. Assuming that no friction exists between the azo-polyimide sample and the elastic sphere tip with radius R, which indents to a displacement d, the applied force can be derived as (Figure 5)
F appl = 4 3 E * R d 3 ,
where E* is the effective elastic modulus. E* can be calculated by measuring Fappl, R, and d:
E * = 3 4 F appl R d 3
In order to evaluate the deformation depth from the surface of the sample, d, one must change the force–distance curve to a tip-sample separation. At the same time, E* is a function of the two materials implied in the interaction, namely, the one of the tip and the one of the sample:
1 E * = 1 − ν tip 2 E tip + 1 − ν sample 2 E sample
where Etip is the elastic modulus of the tip, Esample is the elastic modulus of the sample, νtip is the Poisson’s ratio of the tip, and νsample is the Poisson’s ratio of the sample. The Poisson’s ratio for the Si AFM tip was set at 0.27 [62] and for azo-polyimide sample was set at 0.35 [63,64]. Knowing E*, Etip, νtip, and νsample, Esample can be back-calculated with the formula
E sample = 1 − ν sample 2 1 E * − 1 − ν tip 2 E tip
In this way, the map of the sample’s stiffness/elasticity can be simultaneously acquired through the adhesion force map with the topographic sample information, locally resolving the distribution of adhesion and elasticity on the investigated surface.

Appendix C

Nanomaterials 11 00812 g0a1 550
Figure A1. Raman spectra recorded on pristine and irradiated AzoPI film surfaces.
Figure A1. Raman spectra recorded on pristine and irradiated AzoPI film surfaces.
Nanomaterials 11 00812 g0a1

References

  1. Ghosh, M.K. Polyimides: Fundamentals and Applications; Ghosh, M.K., Mittal, K.L., Eds.; Marcel Dekker: New York, NY, USA, 1996; ISBN 0-8247-9466-4. [Google Scholar]
  2. Wang, D.H.; Lee, K.M.; Yu, Z.; Koerner, H.; Vaia, R.A.; White, T.J.; Tan, L.-S. Photomechanical Response of Glassy Azobenzene Polyimide Networks. Macromolecules 2011, 44, 3840–3846. [Google Scholar] [CrossRef]
  3. Schab-Balcerzak, E.; Siwy, M.; Jarzabek, B.; Kozanecka-Szmigiel, A.; Switkowski, K.; Pura, B. Post and prepolymerization strategies to develop novel photochromic poly(esterimide)s. J. Appl. Polym. Sci. 2011, 120, 631–643. [Google Scholar] [CrossRef]
  4. Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: Basics and current trends. J. Mater. Chem. 2012, 22, 286–300. [Google Scholar] [CrossRef]
  5. Yu, Y.; Nakano, M.; Shishido, A.; Shiono, T.; Ikeda, T. Effect of Cross-linking Density on Photoinduced Bending Behavior of Oriented Liquid-Crystalline Network Films Containing Azobenzene. Chem. Mater. 2004, 16, 1637–1643. [Google Scholar] [CrossRef]
  6. Nikolova, L.; Ramanujam, P. Polarization Holography; Cambridge University Press: Cambridge, UK, 2009; ISBN 9781498775809. [Google Scholar]
  7. Todorov, T.; Nikolova, L.; Tomova, N. Polarization holography 1: A new high-efficiency organic material with reversible photoinduced birefringence. Appl. Opt. 1984, 23, 4309–4312. [Google Scholar] [CrossRef] [PubMed]
  8. Todorov, T.; Nikolova, L.; Tomova, N. Polarization holography 2: Polarization holographic gratings in photoanisotropic materials with and without intrinsic birefringence. Appl. Opt. 1984, 23, 4588–4591. [Google Scholar] [CrossRef] [PubMed]
  9. Schab-Balcerzak, E.; Sobolewska, A.; Miniewicz, A. Comparative studies of newly synthesized azo-dyes bearing poly(esterimide)s with their poly(etherimide) analogues. Light-induced optical anisotropy. Opt. Mater. 2008, 31, 405–411. [Google Scholar] [CrossRef]
  10. Sava, I.; Sacarescu, L.; Stoica, I.; Apostol, I.; Damian, V.; Hurduc, N. Photochromic properties of polyimide and polysiloxane azopolymers. Polym. Int. 2009, 58, 163–170. [Google Scholar] [CrossRef]
  11. Sava, I.; Hurduc, N.; Sacarescu, L.; Apostol, I.; Damian, V. Study of the nanostructuration capacity of some azopolymers with rigid or flexible chains. High Perform. Polym. 2013, 25, 13–24. [Google Scholar] [CrossRef]
  12. Sava, I.; Resmerita, A.-M.; Lisa, G.; Damian, V.; Hurduc, N. Synthesis and photochromic behavior of new polyimides containing azobenzene side groups. Polymer. 2008, 49, 1475–1482. [Google Scholar] [CrossRef]
  13. Sava, I.; Burescu, A.; Stoica, I.; Musteata, V.; Cristea, M.; Mihaila, I.; Pohoata, V.; Topala, I. Properties of some azo-copolyimide thin films used in the formation of photoinduced surface relief gratings. RSC Adv. 2015, 5, 10125–10133. [Google Scholar] [CrossRef]
  14. Bujak, K.; Sava, I.; Stoica, I.; Tiron, V.; Topala, I.; Węgłowski, R.; Schab-Balcerzak, E.; Konieczkowska, J. Photoinduced properties of “T-type” polyimides with azobenzene or azopyridine moieties. Eur. Polym. J. 2020, 126, 109563. [Google Scholar] [CrossRef]
  15. Schab-Balcerzak, E.; Sapich, B.; Stumpe, J. Photoinduced optical anisotropy in new poly (amide imide) s with azobenzene units. Polymer 2005, 46, 49–59. [Google Scholar] [CrossRef]
  16. Schab-Balcerzak, E.; Sobolewska, A.; Miniewicz, A.; Jurusik, J.; Jarzabek, B. Photoinduced Holographic Gratings in Azobenzene-Functionalized Poly(amideimide)s. Polym. J. 2007, 39, 659–669. [Google Scholar] [CrossRef] [Green Version]
  17. Konieczkowska, J.; Schab-Balcerzak, E.; Siwy, M.; Switkowski, K.; Kozanecka-Szmigiel, A. Large and highly stable photoinduced birefringence in poly(amideimide)s with two azochromophores per structural unit. Opt. Mater. 2015, 39, 199–206. [Google Scholar] [CrossRef]
  18. Konieczkowska, J.; Janeczek, H.; Malecki, J.G.; Schab-Balcerzak, E. The comprehensive approach towards study of (azo)polymers fragility parameter: Effect of architecture, intra- and intermolecular interactions and backbone conformation. Eur. Polym. J. 2018, 109, 489–498. [Google Scholar] [CrossRef]
  19. Bujak, K.; Kozanecka-Szmigiel, A.; Schab-Balcerzak, E.; Konieczkowska, J. Azobenzene Functionalized “T-Type” Poly (Amide Imide) s vs. Guest-Host Systems—A Comparative Study of Structure-Property Relations. Materials 2020, 13, 1912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Hurduc, N.; Donose, B.C.; Macovei, A.; Paius, C.; Ibanescu, C.; Scutaru, D.; Hamel, M.; Branza-Nichita, N.; Rocha, L. Direct observation of athermal photofluidisation in azo-polymer films. Soft Matter 2014, 10, 4640–4647. [Google Scholar] [CrossRef] [PubMed]
  21. Hurduc, N.; Donose, B.C.; Rocha, L.; Ibanescu, C.; Scutaru, D. Azo-polymers photofluidisation—A transient state of matter emulated by molecular motors. RSC Adv. 2016, 6, 27087–27093. [Google Scholar] [CrossRef]
  22. Stoica, I.; Epure, L.; Sava, I.; Damian, V.; Hurduc, N. An atomic force microscopy statistical analysis of laser-induced azo-polyimide periodic tridimensional nanogrooves. Microsc. Res. Tech. 2013, 76, 914–923. [Google Scholar] [CrossRef]
  23. Sava, I.; Stoica, I.; Mihaila, I.; Pohoata, V.; Topala, I.; Stoian, G.; Lupu, N. Nanoscale analysis of laser-induced surface relief gratings on azo-copolyimide films before and after gold coating. Polym. Test. 2018, 72, 407–415. [Google Scholar] [CrossRef]
  24. Damian, V.; Resmerita, E.; Stoica, I.; Ibanescu, C.; Sacarescu, L.; Rocha, L.; Hurduc, N. Surface relief gratings induced by pulsed laser irradiation in low glass-transition temperature azopolysiloxanes. J. Appl. Polym. Sci. 2014, 131, 41015. [Google Scholar] [CrossRef] [Green Version]
  25. Pederzoli, M.; Pittner, J.; Barbatti, M.; Lischka, H. Nonadiabatic Molecular Dynamics Study of the cis—Trans Photoisomerization of Azobenzene Excited to the S 1 State. J. Phys. Chem. A 2011, 115, 11136–11143. [Google Scholar] [CrossRef]
  26. Ootani, Y.; Satoh, K.; Nakayama, A.; Noro, T.; Taketsugu, T. Ab initio molecular dynamics simulation of photoisomerization in azobenzene in the nπ∗ state. J. Chem. Phys. 2009, 131, 194306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Biswas, M.; Burghardt, I. Azobenzene Photoisomerization-Induced Destabilization of B-DNA. Biophys. J. 2014, 107, 932–940. [Google Scholar] [CrossRef] [Green Version]
  28. Wei-Guang Diau, E. A New Trans-to-Cis Photoisomerization Mechanism of Azobenzene on the S 1 (n,π*) Surface. J. Phys. Chem. A 2004, 108, 950–956. [Google Scholar] [CrossRef]
  29. Chami, F.; Wilson, M.R. Molecular Order in a Chromonic Liquid Crystal: A Molecular Simulation Study of the Anionic Azo Dye Sunset Yellow. J. Am. Chem. Soc. 2010, 132, 7794–7802. [Google Scholar] [CrossRef]
  30. Böckmann, M.; Peter, C.; Site, L.D.; Doltsinis, N.L.; Kremer, K.; Marx, D. Atomistic Force Field for Azobenzene Compounds Adapted for QM/MM Simulations with Applications to Liquids and Liquid Crystals. J. Chem. Theory Comput. 2007, 3, 1789–1802. [Google Scholar] [CrossRef] [PubMed]
  31. Carlescu, I.; Simion, A.; Epure, E.L.; Lisa, G.; Scutaru, D. Self-assembled star-shaped liquid crystals based on 1,3,5-trihydroxybenzene with pendant alkyloxylated azobenzene arms. Liq. Cryst. 2020, 47, 1852–1862. [Google Scholar] [CrossRef]
  32. Georgiev, A.; Kostadinov, A.; Ivanov, D.; Dimov, D.; Stoyanov, S.; Nedelchev, L.; Nazarova, D.; Yancheva, D. Synthesis, spectroscopic and TD-DFT quantum mechanical study of azo-azomethine dyes. A laser induced trans-cis-trans photoisomerization cycle. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 192, 263–274. [Google Scholar] [CrossRef]
  33. Epure, E.-L.; Vasiliu, T.; Hurduc, N.; Neamțu, A. Molecular modeling study concerning the self-assembly capacity of some photosensitive amphiphilic polysiloxanes. J. Mol. Liq. 2020, 300, 112298. [Google Scholar] [CrossRef]
  34. Xia, S.-H.; Cui, G.; Fang, W.-H.; Thiel, W. How Photoisomerization Drives Peptide Folding and Unfolding: Insights from QM/MM and MM Dynamics Simulations. Angew. Chem. Int. Ed. 2016, 55, 2067–2072. [Google Scholar] [CrossRef] [Green Version]
  35. Böckmann, M.; Doltsinis, N.L. Towards understanding photomigration: Insights from atomistic simulations of azopolymer films explicitly including light-induced isomerization dynamics. J. Chem. Phys. 2016, 145, 154701. [Google Scholar] [CrossRef] [PubMed]
  36. Pawlik, G.; Mitus, A.C. Photoinduced Mass Transport in Azo-Polymers in 2D: Monte Carlo Study of Polarization Effects. Materials 2020, 13, 4724. [Google Scholar] [CrossRef]
  37. Juan, M.L.; Plain, J.; Bachelot, R.; Royer, P.; Gray, S.K.; Wiederrecht, G.P. Stochastic model for photoinduced surface relief grating formation through molecular transport in polymer films. Appl. Phys. Lett. 2008, 93, 153304. [Google Scholar] [CrossRef]
  38. Stiller, B.; Karageorgiev, P.; Geue, T.; Morawetz, K.; Saphiannikova, M.; Mechau, N.; Neher, D. Optically induced mass transport studied by scanning near-field optical - and atomic force microscopy. Phys. Low Dimens. Struct. 2004, 1/2, 129–138. [Google Scholar]
  39. Sadegh Hassani, S.; Daraee, M.; Sobat, Z. Application of atomic force microscopy in adhesion force measurements. J. Adhes. Sci. Technol. 2021, 35, 221–241. [Google Scholar] [CrossRef]
  40. Krotil, H.-U.; Stifter, T.; Waschipky, H.; Weishaupt, K.; Hild, S.; Marti, O. Pulsed force mode: A new method for the investigation of surface properties. Surf. Interface Anal. 1999, 27, 336–340. [Google Scholar] [CrossRef]
  41. Exploring Nanomechanical Properties of Materials with Atomic Force Microscopy, NT-MDT Spectrum Instruments Application Note no. 085. 2017. Available online: https://www.ntmdt-si.com/resources/applications/exploring-nanomechanical-properties-of-materials-with-atomic-force-microscopy (accessed on 22 February 2021).
  42. Expanding Atomic Force Microscopy with HybriD Mode Imaging, NT-MDT Spectrum Instruments Application Note no. 087/2017. Available online: https://www.ntmdt-si.com/resources/applications/expanding-atomic-force-microscopy-with-hybrid-mode-imaging (accessed on 22 February 2021).
  43. Quantitative Nanomechanical Measurements in HybriD Mode Atomic Force Microscopy, NT-MDT Spectrum Instruments Application Note no. 090. 2017. Available online: https://www.ntmdt-si.com/resources/applications/quantitative-nanomechanical-measurements-in-hybrid-mode-atomic-force-microscopy (accessed on 22 February 2021).
  44. Park PinPointTM Mode. Available online: https://parksystems.com/files/pinpoint_mode_brochure.pdf (accessed on 22 February 2021).
  45. Constantin, C.-P.; Sava, I.; Damaceanu, M.-D. Structural Chemistry-Assisted Strategy toward Fast Cis–Trans Photo/Thermal Isomerization Switch of Novel Azo-Naphthalene-Based Polyimides. Macromolecules 2021, 54, 1517–1538. [Google Scholar] [CrossRef]
  46. Materials Studio 4.0; DMol3, Forcite and Amorphous Cell Module; Accelrys Software Inc.: San Diego, CA, USA, 2005.
  47. Miniewicz, A.; Sahraoui, B.; Schab-Balcerzak, E.; Sobolewska, A.; Mitus, A.C.; Kajzar, F. Pulsed-Laser Grating Recording in Organic Materials Containig Azobenzene Derivatives. Nonlinear Opt. Quantum Opt. 2006, X, 1–8. [Google Scholar]
  48. Kim, S.; Park, S.; Lee, W.; Kwon, O.; Kim, S.U.; Choi, Y.; Yoon, M.; Park, J.; Kim, Y. Origin of macroscopic adhesion in organic light-emitting diodes analyzed at different length scales. Sci. Rep. 2018, 8, 1–7. [Google Scholar] [CrossRef]
  49. Othonos, A.; Kalli, K.; Pureur, D.; Mugnier, A. Fibre Bragg Gratings. In Wavelength Filters in Fibre Optics; Springer: Berlin Germany, 2006; Volume 123, pp. 189–269. ISBN 3540317694. [Google Scholar]
  50. Lagugné-Labarthet, F.; Buffeteau, T.; Sourisseau, C. Molecular orientations in azopolymer holographic diffraction gratings as studied by Raman confocal microspectroscopy. J. Phys. Chem. B 1998, 102, 5754. [Google Scholar] [CrossRef]
  51. Stoica, I.; Hurduc, N. Structuring of Polymer Surfaces via Laser Irradiation as a Tool for Micro-and Nanotechnologies. In Electromagnetic Radiation in Analysis and Design of Organic Materials; Dorohoi, D.O., Barzic, A.I., Aflori, M., Eds.; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2017; Chapter 12; pp. 191–206. ISBN 9781498775809. [Google Scholar]
  52. Barrett, C.J.; Natansohn, A.L.; Rochon, P.L. Mechanism of Optically Inscribed High-Efficiency Diffraction Gratings in Azo Polymer Films. J. Phys. Chem. 1996, 100, 8836–8842. [Google Scholar] [CrossRef]
  53. Wu, X.; Ngan Nguyen, T.T.; Ledoux-Rak, I.; Thanh Nguyen, C.; Diep, N. Optically Accelerated Formation of One- and Two-Dimensional Holographic Surface Relief Gratings on DR1/PMMA. In Holography—Basic Principles and Contemporary Applications; InTech: Rijeka, Croatia, 2013. [Google Scholar]
  54. Wu, X. Fabrication of 1D, 2D and 3D polymer-based periodic structures by mass transport effect. Ph.D. Thesis, École Normale Supérieure de Cachan—ENS Cachan, Paris, France, 2013. [Google Scholar]
  55. Viswanathan, N.K.; Balasubramanian, S.; Li, L.; Kumar, J.; Tripathy, S.K. Surface-Initiated Mechanism for the Formation of Relief Gratings on Azo-Polymer Films. J. Phys. Chem. B 1998, 102, 6064. [Google Scholar] [CrossRef]
  56. Sdr Parameters and Its Applications in Characterizing Surface Data. Available online: https://www.azonano.com/article.aspx?ArticleID=5137 (accessed on 2 March 2021).
  57. ISO 25178-2:2012 Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. 2012. Available online: https://www.iso.org/standard/42785.html (accessed on 21 March 2021).
  58. Stoica, I.; Barzic, A.I.; Hulubei, C.; Timpu, D. Statistical analysis on morphology development of some semialicyclic polyimides using atomic force microscopy. Microsc. Res. Tech. 2013, 76, 503–513. [Google Scholar] [CrossRef] [PubMed]
  59. Reifenberger, R. Fundamentals of Atomic Force Microscopy Part I: Foundations; Lessons from Nanoscience: A Lecture Notes Series; World Scientific Publishing: Singapore, 2015; Volume 4, ISBN 978-981-4630-34-4. [Google Scholar]
  60. Park Systems Introduces PinPointTM Nanomechanical Mode to Characterize Nano Mechanical Properties of Materials and Biological Cells. Available online: https://parksystems.com/company/news/press-release/450-nanomechanical-mode-to-characterize-nano-mechanical (accessed on 21 March 2021).
  61. Collagen Fibrils Imaging in Liquid Using Park NX10 Atomic Force Microscope PinPointTM Nanomechanical Mode; Park Atomic Force Microscopy; Application note #4. Available online: https://parksystems.com/applications/life-science/micro-and-molecular-biology/607-collagen-fibrils-imaging-using-park-nx10-atomic-force-microscope-pinpoint-nanomechanical-mode (accessed on 14 March 2021).
  62. Cao, X.; Gan, X.; Peng, Y.; Wang, Y.; Zeng, X.; Lang, H.; Deng, J.; Zou, K. An ultra-low frictional interface combining FDTS SAMs with molybdenum disulfide. Nanoscale 2018, 10, 378–385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  63. Lin, Y.C.; Peng, X.Y.; Wang, L.C.; Lin, Y.L.; Wu, C.H.; Liang, S.C. Residual stress in CIGS thin film solar cells on polyimide: Simulation and experiments. J. Mater. Sci. Mater. Electron. 2014, 25, 461–465. [Google Scholar] [CrossRef]
  64. Blösch, P.; Güttler, D.; Chirila, A.; Tiwari, A.N. Optimization of Ti/TiN/Mo back contact properties for Cu (In,Ga)Se 2 solar cells on polyimide foils. Thin Solid Film. 2011, 519, 7453–7457. [Google Scholar] [CrossRef]
  65. Yadavalli, N.S. Advances in Experimental Methods to Probe Surface Relief Grating Formation Mechanism in Photosensitive Materials. Ph.D. Thesis, University of Potsdam, Postdam, Germany, 2014. [Google Scholar]
  66. Zong, C.; Zhao, Y.; Ji, H.; Han, X.; Xie, J.; Wang, J.; Cao, Y.; Jiang, S.; Lu, C. Tuning and Erasing Surface Wrinkles by Reversible Visible-Light-Induced Photoisomerization. Angew. Chem. Int. Ed. 2016, 55, 3931–3935. [Google Scholar] [CrossRef]
  67. Bian, S.; Williams, J.M.; Kim, D.Y.; Li, L.; Balasubramanian, S.; Kumar, J.; Tripathy, S. Photoinduced surface deformations on azobenzene polymer films. J. Appl. Phys. 1999, 86, 4498–4508. [Google Scholar] [CrossRef]
  68. Srikhirin, T.; Laschitsch, A.; Neher, D.; Johannsmann, D. Light-induced softening of azobenzene dye-doped polymer films probed with quartz crystal resonators. Appl. Phys. Lett. 2000, 77, 963–965. [Google Scholar] [CrossRef]
  69. Mechau, N.; Neher, D.; Börger, V.; Menzel, H.; Urayama, K. Optically driven diffusion and mechanical softening in azobenzene polymer layers. Appl. Phys. Lett. 2003, 81, 4715–4717. [Google Scholar] [CrossRef]
  70. Mechau, N.; Saphiannikova, M.; Neher, D. Dielectric and mechanical properties of azobenzene polymer layers under visible and ultraviolet irradiation. Macromolecules 2005, 38, 3894–3902. [Google Scholar] [CrossRef]
  71. Gherab, K.N.; Gatri, R.; Hank, Z.; Dick, B.; Kutta, R.J.; Winter, R.; Luc, J.; Sahraoui, B.; Fillaut, J.L. Design and photoinduced surface relief grating formation of photoresponsive azobenzene based molecular materials with ruthenium acetylides. J. Mater. Chem. 2010, 20, 2858–2864. [Google Scholar] [CrossRef] [Green Version]
  72. Wang, X. Azo Polymers: Synthesis, Functions and Applications; Springer: Berlin, Germany, 2017; ISBN 9783662534229. [Google Scholar]
  73. Di Florio, G.; Bründermann, E.; Yadavalli, N.S.; Santer, S.; Havenith, M. Graphene Multilayer as Nanosized Optical Strain Gauge for Polymer Surface Relief Gratings. Nano Lett. 2014, 14, 5754–5760. [Google Scholar] [CrossRef]
  74. Di Florio, G.; Bründermann, E.; Yadavalli, N.S.; Santer, S.; Havenith, M. Polarized 3D Raman and nanoscale near-field optical microscopy of optically inscribed surface relief gratings: Chromophore orientation in azo-doped polymer films. Soft Matter 2014, 10, 1544. [Google Scholar] [CrossRef]
Nanomaterials 11 00812 g001 550
Figure 1. Chemical structure of the novel azo-naphthalene-based polyimide, AzoPI, used in this study.
Figure 1. Chemical structure of the novel azo-naphthalene-based polyimide, AzoPI, used in this study.
Nanomaterials 11 00812 g001
Nanomaterials 11 00812 g002 550
Figure 2. Pulsed laser irradiation through a phase mask setting, with a detail on the formation of interference image on the azo-naphthalene-based polyimide surface.
Figure 2. Pulsed laser irradiation through a phase mask setting, with a detail on the formation of interference image on the azo-naphthalene-based polyimide surface.
Nanomaterials 11 00812 g002
Nanomaterials 11 00812 g003 550
Figure 3. Height 3D atomic force microscopy (AFM) images and corresponding cross-section profiles for azo-polyimide irradiated using different laser energy density/number of pulses of irradiation: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h).
Figure 3. Height 3D atomic force microscopy (AFM) images and corresponding cross-section profiles for azo-polyimide irradiated using different laser energy density/number of pulses of irradiation: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h).
Nanomaterials 11 00812 g003
Nanomaterials 11 00812 g004 550
Figure 4. Height histograms and surface bearing area ratio curves corresponding to height AFM images for azo-polyimide irradiated using different laser energy density/number of pulses of irradiation: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h).
Figure 4. Height histograms and surface bearing area ratio curves corresponding to height AFM images for azo-polyimide irradiated using different laser energy density/number of pulses of irradiation: 10 mJ/cm2/10 pulses (a,b), 10 mJ/cm2/100 pulses (c,d), 45 mJ/cm2/10 pulses (e,f), 45 mJ/cm2/100 pulses (g,h).
Nanomaterials 11 00812 g004
Nanomaterials 11 00812 g005 550
Figure 5. Working mechanism of PinPoint Nanomechanical mode: the tip of the cantilever is moved at each of 256 × 256 points along a sample’s surface, and the feedback system controls the approach and retraction of a probe, allowing the acquirer of both surface topography and force–distance curves, and further to extract the mechanical property data.
Figure 5. Working mechanism of PinPoint Nanomechanical mode: the tip of the cantilever is moved at each of 256 × 256 points along a sample’s surface, and the feedback system controls the approach and retraction of a probe, allowing the acquirer of both surface topography and force–distance curves, and further to extract the mechanical property data.
Nanomaterials 11 00812 g005
Nanomaterials 11 00812 g006 550
Figure 6. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus images and representative cross-section profiles taken along the middle line obtained for pristine azo-polyimide.
Figure 6. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus images and representative cross-section profiles taken along the middle line obtained for pristine azo-polyimide.
Nanomaterials 11 00812 g006
Nanomaterials 11 00812 g007 550
Figure 7. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus AFM images and corresponding cross-section profiles mediated from the presented three lines obtained for azo-polyimide irradiated with a laser energy density of 45 mJ/cm2 and 10 pulses.
Figure 7. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus AFM images and corresponding cross-section profiles mediated from the presented three lines obtained for azo-polyimide irradiated with a laser energy density of 45 mJ/cm2 and 10 pulses.
Nanomaterials 11 00812 g007
Nanomaterials 11 00812 g008 550
Figure 8. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus images and corresponding cross-section profiles mediated from the presented three lines obtained for azo-polyimide irradiated with a laser energy density of 45 mJ/cm2 and 100 pulses.
Figure 8. AFM PinPoint combined height, adhesion force, deformation, and Young’s modulus images and corresponding cross-section profiles mediated from the presented three lines obtained for azo-polyimide irradiated with a laser energy density of 45 mJ/cm2 and 100 pulses.
Nanomaterials 11 00812 g008
Nanomaterials 11 00812 g009 550
Figure 9. Molecular modeling of the photo-isomerization process of the azo-naphthalene groups: (a) minimum energy conformations of a AzoPI repeating unit in trans and cis states; (b) three-dimensional view of one amorphous cell for the AzoPI in stage I, stage II, and stage III (three polymer chains inside, each containing 10 repeating units; the grey surface indicates the Van der Waals surface, the blue surface indicates the void surface).
Figure 9. Molecular modeling of the photo-isomerization process of the azo-naphthalene groups: (a) minimum energy conformations of a AzoPI repeating unit in trans and cis states; (b) three-dimensional view of one amorphous cell for the AzoPI in stage I, stage II, and stage III (three polymer chains inside, each containing 10 repeating units; the grey surface indicates the Van der Waals surface, the blue surface indicates the void surface).
Nanomaterials 11 00812 g009
Nanomaterials 11 00812 g010 550
Figure 10. Evolution in time of the mean square displacement function of the AzoPI backbones and corresponding azo segments in stage I, stage II, and stage III.
Figure 10. Evolution in time of the mean square displacement function of the AzoPI backbones and corresponding azo segments in stage I, stage II, and stage III.
Nanomaterials 11 00812 g010
Nanomaterials 11 00812 g011 550
Figure 11. Evolution in time of total dipole moment (μ) and of the x, y, and z components of the dipole moment (μx, μy, and μz, respectively) of the azo segments (C–N=N–C) of AzoPI in stage I, stage II, and stage III.
Figure 11. Evolution in time of total dipole moment (μ) and of the x, y, and z components of the dipole moment (μx, μy, and μz, respectively) of the azo segments (C–N=N–C) of AzoPI in stage I, stage II, and stage III.
Nanomaterials 11 00812 g011
Table
Table 1. 3D roughness parameters obtained from AFM images of the investigated azo-polyimide samples (energy density of 10 or 45 mJ/cm2 and variable number of laser pulses 10 or100).
Table 1. 3D roughness parameters obtained from AFM images of the investigated azo-polyimide samples (energy density of 10 or 45 mJ/cm2 and variable number of laser pulses 10 or100).
ParameterSample
AzoPI 10/10AzoPI 10/100AzoPI 45/10AzoPI 45/100
Height parameters
Sq (nm)0.40.73216.15928.723
Shape parameters
Ssk0.466−0.2840.7620.343
Sku5.4663.0612.3543.193
Spatial parameters
Stdi0.3880.4180.1930.407
Hybrid parameters
Sdr (%)0.005420.009811.4965.342
Functional indexes
Sbi0.1130.3080.7940.429
Sci1.4641.3461.8391.671
Svi0.08550.1310.0460.096
Functional volume parameters
Vmp (nm3/nm2)0.02320.02420.5621.62
Vmc (nm3/nm2)0.3650.66413.30025.4
Vvc (nm3/nm2)0.4630.87525.40036.6
Vvv (nm3/nm2)0.03340.0960.7542.75
Sq: root mean square roughness of the surface; Ssk: skewness of height distribution; Sku: kurtosis of height distribution; Stdi: surface texture direction index; Sdr: surface area ratio; Sbi: surface bearing index; Sci: core fluid retention index; Svi: valley fluid retention index; Vmp: peak material volume; Vmc: core material volume; Vvc: core void volume; Vvv: valley void volume.
Table
Table 2. The values of the nanomechanical characteristics (adhesion force, deformation, and Young’s modulus) measured at different positions on the azo-polyimide samples before and after laser irradiation by using AFM PinPoint mode.
Table 2. The values of the nanomechanical characteristics (adhesion force, deformation, and Young’s modulus) measured at different positions on the azo-polyimide samples before and after laser irradiation by using AFM PinPoint mode.
SamplePosition on the SampleNanomechanical Characteristics
Adhesion Force
(nN)		Deformation
(nm)		Young’s Modulus
(MPa)
AzoPIAll over the surface12.6 ± 0.85.1 ± 0.2294.8 ± 20.5
AzoPI 45/10SRG top hills11.6 ± 0.36.3 ± 0.1299.8 ± 5.5
SRG middle slopes6.2 ± 0.78.9 ± 0.1195.1 ± 4.6
SRG bottom valleys12.1 ± 0.16.7 ± 0.1311.0 ± 5.2
SRG base line11.4 ± 0.46.8 ± 0.2302.8 ± 9.1
AzoPI 45/100SRG top hills12.9 ± 1.95.4 ± 0.2294.2 ± 9.0
SRG middle slopes3.2 ± 0.48.9 ± 0.3128.9 ± 8.6
SRG bottom valleys13.3 ± 0.15.1 ± 0.2307.9 ± 12.2
SRG base line12.4 ± 0.35.1 ± 0.1301.9 ± 12.3
Table
Table 3. Predicted parameters for the azo-polyimide systems studied by molecular simulation.
Table 3. Predicted parameters for the azo-polyimide systems studied by molecular simulation.
AzoPI SampleParameter
ρp
(g/cm3)		Vo
(Å3)		Vf
(Å3)		FFVree
(Å)		CED × 107
(cal/m3)
Stage I1.2025,01217,10540.6131.065.8409
Stage II1.1925,02517,64241.3536.555.7983
Stage III1.2124,99316,64939.9828.956.0190
ρp—density of packing; Vo—occupied volume with the atoms being represented by Van der Waals radii; Vf—free volume; FFV = (Vf/(Vo + Vf))∙100—fractional free volume; ree—end-to-end distance of the polymers; CED—cohesive energy density.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Stoica, I.; Epure, E.-L.; Constantin, C.-P.; Damaceanu, M.-D.; Ursu, E.-L.; Mihaila, I.; Sava, I. Evaluation of Local Mechanical and Chemical Properties via AFM as a Tool for Understanding the Formation Mechanism of Pulsed UV Laser-Nanoinduced Patterns on Azo-Naphthalene-Based Polyimide Films. Nanomaterials 2021, 11, 812. https://0-doi-org.brum.beds.ac.uk/10.3390/nano11030812

AMA Style

Stoica I, Epure E-L, Constantin C-P, Damaceanu M-D, Ursu E-L, Mihaila I, Sava I. Evaluation of Local Mechanical and Chemical Properties via AFM as a Tool for Understanding the Formation Mechanism of Pulsed UV Laser-Nanoinduced Patterns on Azo-Naphthalene-Based Polyimide Films. Nanomaterials. 2021; 11(3):812. https://0-doi-org.brum.beds.ac.uk/10.3390/nano11030812

Chicago/Turabian Style

Stoica, Iuliana, Elena-Luiza Epure, Catalin-Paul Constantin, Mariana-Dana Damaceanu, Elena-Laura Ursu, Ilarion Mihaila, and Ion Sava. 2021. "Evaluation of Local Mechanical and Chemical Properties via AFM as a Tool for Understanding the Formation Mechanism of Pulsed UV Laser-Nanoinduced Patterns on Azo-Naphthalene-Based Polyimide Films" Nanomaterials 11, no. 3: 812. https://0-doi-org.brum.beds.ac.uk/10.3390/nano11030812

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop